- 제 1종 오류($\alpha$)
- 귀무가설과 대립가설
- 검정통계량
설명에 앞서 위 개념에 대해 잘 모르신다면, 아래 글을 읽고 오시면 이해하시는데 도움이 될 것입니다 :)
→ (통계 용어) 제 1종 오류, 제 2종 오류, 검정력
유의수준($\alpha$)
제 1종 오류를 범할 최대 허용치
→ 이 값은 사전에 "미리" 오류의 허용 범위를 지정하는 것으로서, "관측치와 무관한 값"입니다.

위의 그림에서 "검정통계량값 2"를 갖는 경우 귀무가설($H_0$)이 기각된다고 할 수 있습니다.
※ 유의수준 95% vs 99%
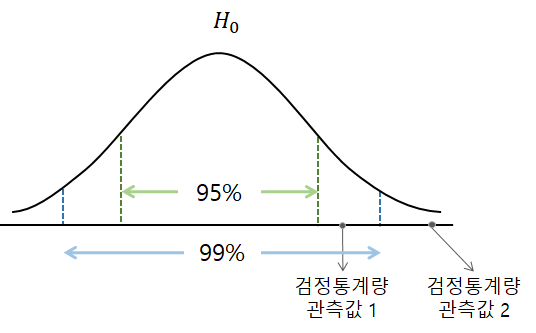
- 95%의 경우가 99% 보다 $H_1$을 지지하는 검정통계량 값을 많이 허용합니다.$\\$
- 99%가 95%보다 $H_0$을 더 옹호합니다.
유의확률 (p-value)
귀무가설($H_0$)을 기각할 수 있는 최소한의 유의수준
→ Data에서 관측된 검정통계량 값이 귀무가설($H_0$)를 지지하는 정도가 강한지를 나타냅니다.
즉, 이 값이 작을수록 다음과 같은 특징을 갖습니다.
- $H_0$의 지지율이 감소.
- $H_0$을 기각하는 결정이 잘못되었을 가능성이 감소.
→ 계산 결과 나온 검정통계량 값을 기준값으로 사용합니다.

※ p-value < $\alpha$ → $H_0$ 기각
p-value값이 작을수록 $\alpha$의 범위가 증가합니다.
즉, 이것은 $H_0$을 기각해도 될 확률이 증가하며
= $H_0$ 지지율이 감소합니다.
반응형
'Statistics' 카테고리의 다른 글
| (수리 통계) Gamma distribution (감마 분포) (0) | 2021.12.20 |
|---|---|
| (통계 용어) 자유도 (Degree of Freedom)란? (0) | 2021.03.30 |
| (통계 용어) 확률 변수, 확률 분포 Etc (0) | 2021.03.22 |
| (통계 용어) 표준 편차 vs 표준오차 (0) | 2021.03.22 |
| (통계 용어) 검정력 (Power) (0) | 2021.03.22 |

