대립 가설($H_1$) : 주장하고자 하는 가설
귀무 가설($H_0$) : 그것에 반하는 가설
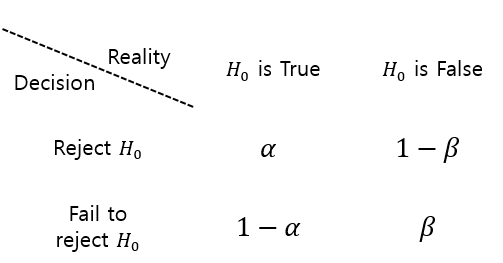
제 1종 오류 - $\alpha$ or $\alpha(\theta)$
귀무가설($H_0$)이 참일 때, 귀무가설($H_0$)를 기각하는 오류 입니다.
제 2종 오류 - $\beta$ or $\beta(\theta)$
대립가설($H_1$)이 참일 때, 귀무가설($H_0$)를 기각하는 채택하는 오류 입니다.
검정력 - $power$ or $1-\beta(\theta)$
대립가설($H_1$)이 참일 때, 귀무가설($H_0$)를 기각하는 오류 입니다.
(검정력, 검정 통계량에 관한 내용은 따로 정리하였습니다.)
※ 위 세 값을 식으로 표현하면 다음과 같습니다.
제 1종 오류 : $P(H_0 기각 | H_0 참)$
제 2종 오류 : $P(H_0 채택 | H_1 참)$
검정력 : $P(H_0 기각 | H_1 참)$
$H_0$ : $\theta = \theta_0$ vs $H_1$ : $\theta > \theta_0$
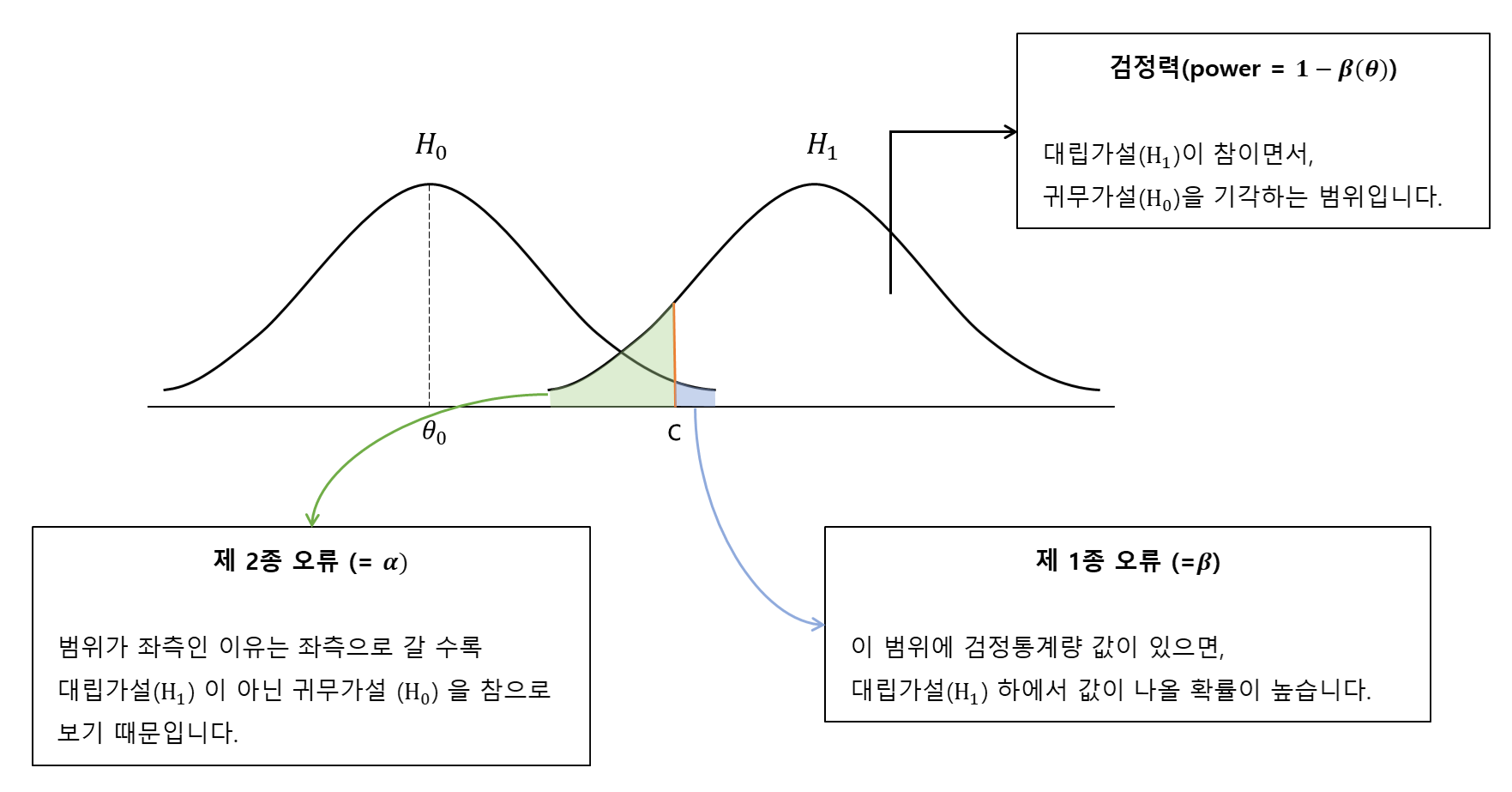
* 제 1종 오류가 $\alpha$, 제 2종 오류가 $\beta$ 입니다!
- 가설이 양측인 경우는 $H_1$ 그래프가 양쪽으로 그려집니다.
- 가설의 부호가 반대인 경우에는 $H_1$ 그래프가 반대쪽에 그려집니다.
특징
- 제 1종 오류와 제 2종 오류는 동시에 감소가 불가능합니다. $\\$ 따라서 더 심각한 오류인 제 1종 오류($\alpha$)를 기준으로 잡습니다.
※ 제 1종 오류가 더 심각한 오류인 이유는 기존 주장(귀무가설 $H_0$)이 옳음에도 기존 주장(귀무가설 $H_0$)이
잘못된 것으로 판단해 기존의 것을 전부 변화시켜야 하는 부담이 크기 때문입니다.
예를 들어 한 공장에서 기계를 전부 바꿔야 한다는 주장이 나왔다고 합시다.
이럴 경우 가설의 설정을 다음과 같이 할 수 있습니다.
$H_0$ : 공장의 기계를 안 바꾸는 게 낫다. vs $H_1$ : 공자의 기계를 바꾸는게 낫다.
여기서 제1종 오류의 경우 : $H_0$의 주장이 맞음에도 $H_1$를 따르게 되어
기계를 바꿔야 하는 금액적 손실이 이뤄질 수 있습니다.
그러나 제2종 오류의 경우 : $H_1$이 주장이 맞지만 $H_0$을 채택하여
비록 새롭게 주장한 내용이 맞더라도 기계를 바꿔야 하는 경제적 부담은 없게 됩니다.
'Statistics' 카테고리의 다른 글
| (통계 용어) 유의수준 and 유의확률 (0) | 2021.03.22 |
|---|---|
| (통계 용어) 확률 변수, 확률 분포 Etc (0) | 2021.03.22 |
| (통계 용어) 표준 편차 vs 표준오차 (0) | 2021.03.22 |
| (통계 용어) 검정력 (Power) (0) | 2021.03.22 |
| (통계 용어) 통계량, 추정량, 추정치 (0) | 2021.03.16 |


