표준편차 와 표준오차
통계를 공부하는 사람이라면, 표준편차에 대해 많이 들어봤을 것입니다.
그렇다면 표준오차는 무엇일까요? 표준편차랑 같은 것일까요? 그 차이점에 대해 이야기해보겠습니다.
표준편차 (SD, Standard Deviation)
자료가 평균으로부터 얼마나 퍼져있는지 나타내는 지표
아래의 그림에서 $\sigma$에 해당합니다.

표준오차 (SEM, Standard Error of the Mean)
표본의 평균이 얼마나 모평균에 가까운지 나타내는 지표
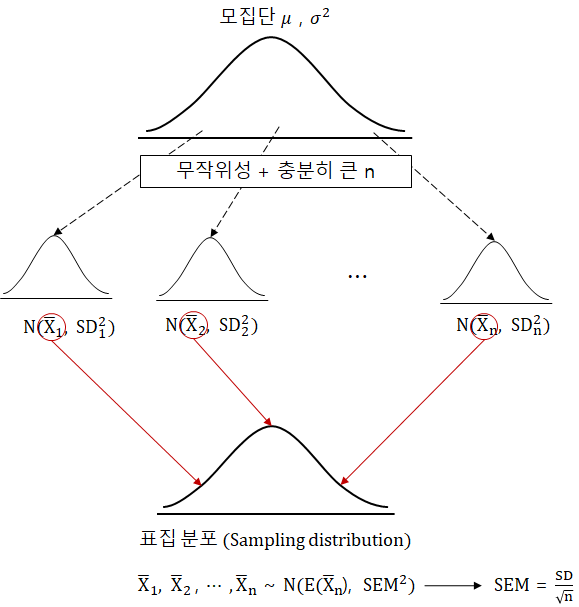
여기서, SEM은 두 가지 특징을 갖습니다.
- 모집단의 변동과 추출된 표본의 개수에 따라 좌우된다. $\\$
- 그러나 실제로는 하나의 표본만 추출하므로, $\\$이 표본의 표준편차(SD)와 표본수를 이용하여 표준오차(SEM)를 추정.
표준편차(SD)와 표준오차(SEM)에 대한 특징들을 몇가지 적어보자면 다음과 같습니다.
º 분산은 계산과정 중 관측값의 단위를 제곱하게 되어 자료해석에 혼란 야기가 가능하여,
자료의 평균과 같은 단위를 사용하는 SD를 이용하는 것이 더 적절합니다.
º 표본 수가 같다면, SD, SEM 무엇을 사용해도 무관합니다.
그러나 다른 경우, 이를 명시하여 정확한 정보 전달이 필요합니다.
º 정규분포를 전제하는 표본에서는 SD : 표본을 구성하는 자료의 변동을 반영
SEM : 표집 분포를 구성하는 평균들의 변동을 반영
º 표본의 특성 기술 시 정규성 검정이 선행된 상태에서 SD를 사용하는 것이 바람직합니다.
그러나 자료에 따라 표본 수를 제시한다면, SEM or C.I(신뢰구간)를 통한 표현도 가능합니다.
º 통계분석 결과를 제시할 때는 SD보다는 표본 수와 함께 SEM을 사용하면,
추정된 모집단들의 직관적인 비교가 표나 그래프를 통해 가능하여 결과해석이 용이합니다.
'Statistics' 카테고리의 다른 글
| (통계 용어) 유의수준 and 유의확률 (0) | 2021.03.22 |
|---|---|
| (통계 용어) 확률 변수, 확률 분포 Etc (0) | 2021.03.22 |
| (통계 용어) 검정력 (Power) (0) | 2021.03.22 |
| (통계 용어) 제 1종 오류, 제 2종 오류, 검정력 (2) | 2021.03.16 |
| (통계 용어) 통계량, 추정량, 추정치 (0) | 2021.03.16 |



