회귀분석이 연속형 변수들에 대해 독립 수와 종속변수 사이의 상관관계를 나타내는 것이라면,
단순 회귀 분석은 독립 변수가 단일 개일 때의 분석을 의미한다. (Wikipedia)
$$y_i = \beta_0 + \beta_1 x_i + \varepsilon_i \\
\varepsilon_i \sim N(0, \sigma^2)$$
목적
$x, y$ 의 관계를 "최대한" 위와 같은 선형 직선의 관계로 나타내고자 하는 것입니다.
그러기 위해 의 관계를 $x, y$ 잘 설명하는 $\beta_0 , \beta_1$을 알아내야 합니다.
하지만 이 값은 실제로 알 수 없는 값으로 최대한 비슷한 값인 $b_0, b_1$을 추정하고 사용하여 위 식과 가장 비슷한 식을 알아내고자하는 것이 목적입니다.
$$y_i = \beta_0 + \beta_1 x_i + \varepsilon_i$$
$$↓$$
$$\hat{y_i} = b_0 + b_1 x_i$$
가정
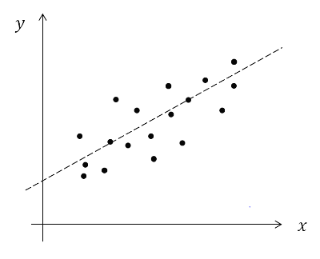
그러나 단순회귀 모형의 데이터는 아래의 그림처럼 생겼기에 완벽하게 선형식으로 표현할 수 없습니다.
그래도 최대한 선형식 관계로 나타내고 싶기에 몇 가지 가정을 만들어 선형식을 만들어냅니다.
(오차를 "왜? 하필!" 이렇게 가정하는지에 대해서는 따로 포스팅하겠습니다. Here!)
1. $x, y$ 는 선형 관계
2. $x$ : 오차 없이 측정 가능한 수학 변수$y$ : 오차를 수반하는 확률 변수(Random Variable)
3. $\varepsilon_i \sim N(0, \sigma^2), \ iid$
· $\varepsilon_i \sim Normal$ : 오차(= $\varepsilon_i$) 는 정규분포를 따른다. → 정규성 (Normality)
· $var(\varepsilon_i) = \sigma^2$ : 오차의 분산이 $x_i$와 관계없이 일정하다. → 등분산성 (Homoscedasicity)
· $\ Cov(\varepsilon_i , \varepsilon_j) = 0 \ \ i≠j$ : 오 차 항은 서로 독립이다. → 독립성 (Independent)
(+ 추가)
· $x$ 의 샘플 수는 2개 이상
· $Cov(X_i , X_j) = 0 \ (i!=j)$ in Multi-Regression
추정
$\beta_0 , \beta_1$는 통계 용어로 모수(Parameter)에 해당하는 값으로, 실제로는 알 수 없는 값입니다.
그러나 회귀분석은 이 $\beta_0 , \beta_1$을 알고 싶어 하는 것으로 진짜 $\beta_0 , \beta_1$ 값은 알 수 없으니 이 값과 비슷한 값을 "추정"하여 나온 값인
$b_0 , b_1$을 사용합니다.
$$\hat {\beta_0} = b_0 \ , \ \hat {\beta_1} = b_1$$
그리고 이 $b_0 , b_1$을 추정하는 가장 유명한 방법은 세 방법이 있습니다. (자세한 내용은 이곳에 있습니다.)
1. Ordinart Least Squares Method (= OLS, 최소제곱법)
2. Maximum Likelihood Estimation Method (= MLE, 최대우도 추정법)
3. Method of Moment Estimation (= MOM, 적률 추정법)
'Regression' 카테고리의 다른 글
| Q-Q plot 정규분포에만 사용할까?? (1) | 2021.04.28 |
|---|---|
| 최우추정법 (MLE, Method of Maximum likelihood Estimation (2) | 2021.04.02 |
| 최소 제곱법 (Least Square Method = OLS) (1) | 2021.04.01 |
| VIF > 10의 의미는 무엇일까? (0) | 2021.03.27 |
| 선형 회귀 모형 가정을 왜 하는가? (1) | 2021.03.15 |

